まず謝罪、そして問題提起
耳目を集めるためにあえてキャッチーなタイトルを付けたことを最初に謝罪します。でもそれは「分光法」という皆が当然理解していると思っている概念に対して、ちょっとでもよいので疑問を持ってもらいたいからです。常識を疑ってみるというのはとても大事なことだと僕は思っています。かのアインシュタインは浸透圧という現象に疑問を持つことで、ブラウン運動を解き明かしました[例えば、米沢富美子, 物理学OnePoint 27 ブラウン運動, 共立出版, 1986]。同じようなことを「分光法」という概念に対して示そうというのがこのエッセイの目的になります。到達点がどこなのか知りたい人は最後まで読んでね!
レオロジーというのは液体の性質である粘性と固体の性質である弾性を区別なく取り扱う力学である[例えば、日本レオロジー学会編, 新講座レオロジー, 日本レオロジー学会, 2014]。流体力学や弾性理論に比べると完成度は低いが、現実の物質・物体はすべからく液体と固体の性質を少しは併せ持っているので、現実の物質・物体をあるがままに取り扱うという意味では究極の力学と言える。特に、粘度の高い液体状物質を取り扱う際には必須で、高分子材料やコンクリートの研究では必修科目となっている。レオロジーにおいて力学情報を得る際、試料に周期的なひずみを加え、その際に発生する応力を波として測定するということをしばしば行う(ひずみと応力の役割は逆転させてもよい)。入力ひずみがサイン波の場合、出力に相当する応力もサイン波になるが、振幅と位相が違ってくる。出力波の振幅と位相から弾性率を複素数として算出する。このような測定を行う装置はレオメーターと呼ばれている。
こうしたレオロジー測定は「分光法」とはかけ離れているように見える。「光」の要素はないし、複素数を値とする分光法はほとんどない。だから、「レオロジー測定は分光の一種だ」、と言うとレオロジーの専門家でも「え?」という反応になる。このエッセイでは「分光法」の概念を再定義することでレオロジー測定などが広義の分光法に属することを示そうと思う。再定義された分光法は「エネルギー保存」の自然な帰結であり、エネルギー保存則に基づくあらゆる議論に影響を与えると考えられる。これは世界の解釈に新たな視点を与えるはずだ。
レオロジー測定と分光法の隔たりは大きすぎるので、とりあえず一つ共通点を示しておこう。複素数の弾性率は入力波の周波数に依存性を持っており、測定の際は入力波の周波数で掃引することになる。横軸に周波数、縦軸に得られ弾性率の実数成分と虚数成分をプロットして表示するというのが標準的なデータ(グラフ)である。これは粘弾性スペクトルと呼ばれる。分光データも通常スペクトルと呼ばれるので、データの表示に関してはレオロジー測定と分光には共通する部分がある。レオロジー界隈の共通認識としては、データは分光法に似ているが、測定は分光法ではない、というところだろうか。
分光法という概念に疑問を持った日
1990年代前半のある日、僕は研究室に配属されたばかりの学部4回生だった。研究室にはX線小角散乱法(Small-angle X-ray Scattering, SAXS)の装置があり、研究室の学生としてその勉強をしていた。SAXSは単色のX線を細く絞ってビームとして試料に照射し、散乱角が10度以下の低角度範囲の散乱強度を収集する実験技術である。低角度での測定は技術的に難しく、デリケートな調整が必要なやっかいな装置である。当時京都大学にいらっしゃった松重和美先生がSAXSと等価なデータを波長掃引によって得るという装置を開発し、その論文を目にした[堀内俊寿, 松重和美: 理学電機ジャーナル, 21, 19(1990)]。SAXSのデータは横軸に散乱ベクトル、縦軸に強度を取ってプロットするのが標準である。散乱ベクトルは$q=2 \pi \sin {\theta}/\lambda$であらわされ、$2\theta$が散乱角度、$\lambda$は波長である。散乱ベクトルは$\theta$が小さい小角散乱の範囲ではおおむね散乱角度に比例する。松重先生は、SAXSデータの横軸を散乱角度ではなくて、波長で変更するということを行ったということである。波長で掃引するというのは、要はプリズムによる分光をX線領域で行った解釈できる。つまり、SAXSは分光法の実験技術でも実行できることを実際に示しているということである。松重先生の研究にとても感銘を受けたが、この実験技術にはいくつか欠点があり、残念ながらマイナーな技術にとどまっている。
2000年頃のある日、僕は理化学研究所播磨研究所でポスドクをしており、SPring-8の小角散乱実験ハッチでビームラインサイエンティストもどきの仕事していた。当時のボスの藤澤哲朗先生が朝の仕事始めに「さ、今日も分光器の調整しようか」と何気におっしゃったのを聞いて、僕は違和感を感じた。藤澤先生の言う「分光器」はSAXSの光学系のことで、彼は散乱実験の装置のことをさも当然のように分光器と呼んだのである。散乱・回折では散乱強度の角度依存性を測定するのであって、プリズムのような分光とは似ていない。とっさに松重先生のお仕事を思い出し、実際に分光の実験技術で置き換えることも可能であるのだから、散乱・回折実験は分光と呼んでもよいのかもしれないと、その場では納得した。
2005年頃、僕は大学で教鞭をとっており、計算機の演習を担当していた。化学系なので、有機分子を計算機上で描くソフトウェアの指導も含まれていた。そういったソフトウェアでは有機分子の立体構造を分子力学法(Melecular Mechanics, MM)で計算して表示するという機能が実装されていることが多い。その紹介をするのが演習内容だった。そのソフトウェアではさらに分子動力学法(Molecular Dynamics, MD)を用いて赤外吸収スペクトルを定性的に描く、という機能があった。定性的なので、ちょっと違和感があるグラフしか出てこないが、ピーク位置はまあまあの信頼性があるという触れ込みだった。MD計算で分光法の予測ができるということに僕は軽いショックを受けた。二つの分野の関連性が良くわからない。僕な中にもやもやしたものが生じた。
これらのエピソードは「分光法とは何か?」という疑問を僕の中に残し、その後20年近くにわたる考察のきっかけとなった。
普通の分光法では何を測定しているのか?
分光法としておそらく最も典型的なのは赤外吸収分光法(Infra-red Spectroscopy, IR)だろう。IRでは赤外線を試料に照射し、赤外線が試料を透過する際の透過率を測定する。赤外線の透過率は強い波長依存性を持つ。そのため、波長に対して透過率という測定値をプロットすることになる。IRでは波長をそのまま横軸にはせずに、波長の逆数である波数を横軸にとり、透過率あるいは透過率の対数を縦軸にとってデータをプロットする。このプロットは赤外吸収スペクトルと呼ばれる。
IRでは試料中の様々な分子内振動の有無と量の情報が得られる。この情報はとりわけ有機分子の場合に有用で、当該分子内の特定の化学結合や化学構造の有無などが議論できるようになる。特定の化学結合や化学構造がどの波数で吸収を起こすかという情報はデータベース的に調査・整理されており、そのデータベースと比べることで、測定対象の分子の特定まで至ることも不可能ではない。また、前節での触れたようにMDを用いて大雑把なIRスペクトルを予測することもできる。
有機化学分野でIRと並んでよく利用される分光法に核磁気共鳴法(Nuclear Magnetic Resonance, NMR)がある。NMRでは試料は強磁場中に静置され、強い電波パルスが照射される。パルス照射の直後から試料は磁場の振動を放射するようになる。この振動を試料の周りに配置されたコイルで検出することで、NMRスペクトルという情報を得ることができる。
NMRは厳密には共鳴現象ではあるが、NMRスペクトルは系中に存在する化学構造(主に水素に関連する化学構造)による「吸収」と磁場信号の「放出」を反映している。横軸はppmという単位だが、これは検出される磁場信号の周波数から算出されるので、横軸の実態は周波数である。
IRやNMRのように分光データの横軸の実体は周波数や波長であり、そのようなデータのグラフは一般的にスペクトルと呼ばれる。横軸が周波数や波長など様々なのはそれぞれの測定の歴史を反映している。ただし、真空中の光速が定数であることから、波長・周波数・波数の間の変換は一義的である。つまり、横軸が波長・周波数・波数のいずれであってもデータの本質は変わらない。なので、横軸の定義に揺らぎがあったとしても、すべてスペクトルと呼んでも構わないことになる。より物理学寄りの議論では横軸としてエネルギーを用いることが多い。エネルギーは$E=h\nu$の関係から振動数と対応付けられるので、波長・周波数・波数との相互変換が可能である。
IRでは赤外線、NMRでは電波を用いるという違いはあるが、いずれも電磁波の一種であり、「光」に分類されるものである。光による吸収を調べるという意味でIRとNMRはともに「分光法」だと解釈できる。しかしながら、小学校の教科書にあるような分光の説明は少々異なる。「プリズムに白色光を入射すると、波長ごとに分かれて虹色が現れる。この現象を分光と呼ぶ。」とある。プリズムに用いるガラスの屈折率には波長依存性があり、その波長依存性を強調する形状がプリズム(三角柱)である。白色光には様々な波長の光が含まれているのだが、それぞれの波長の光に分けることが分光であるという説明は、言葉と現象が1対1に対応しており、説得力がある。そしてこの説明の中に「吸収」という概念が一切登場しないことに注意してほしい。
最も単純なIRでは赤外線光源を赤外線用プリズムで分光し、試料に照射する。あるいは白色の赤外線を試料に照射し、透過した赤外線をプリズムで分光する。なので、分光という技術を使って吸収を測定するというのがIRの基本と言える。単なる分光ではなく、それを利用して赤外線領域の吸収を測定する方法なので、IRは赤外吸収「分光法」と、「法」がついている。英語ではspectroscopyで、「y」で終わることで「法」の意味が付与される。
IRではもはやプリズムが不要だったりするので、実際の測定は分光しないことも多い。つまり、分光法ではあるが、分光は使っていないということである。なので、分光法では分光は必須ではないというややこしいことになっている。
NMRでは最初からプリズムの出番はない。計測された磁場の信号はフーリエ変換を通して周波数に分解され、スペクトルに加工される。NMRも分光法に分類されることから、分光法とは測定値を周波数・波数・波長・エネルギーの関数として整理する技術と解釈した方がよさそうだ。SAXSは波長によって整理することも可能であるのだから、「SAXSは分光の一種であり、SAXSの装置は分光器と呼んでも不自然ではない」かもしれない。同じ理由で、測定値である複素粘弾性率を周波数で整理するレオロジー測定も分光法の一種であると解釈してもよいかもしれない。いや、そこまで極論するのはちょっとやりすぎな気もする。
このセクションをまとめると、分光法で得られる情報の横軸は、周波数・波数・波長・エネルギーのいずれかで、そのような情報(グラフ)はスペクトル(分光データ)と呼ばれている、ということになる。
電磁波の名前
IRやNMRの話の時に、赤外線も電波も電磁波に分類されるので広い意味では光であることを指摘した。電磁波が波長によって呼称が変化することは周知の事実である。ではなぜ呼称が変化するのだろうか?
Maxwellの電磁方程式を解くことで電磁波という概念が導かれ、それは光、特に可視光をうまく説明した。同時に電磁波の波長を変えることで、電波も電磁波であることが明らかになった。つまり、可視光と電波は元々は別物と考えらえれていたが、波長の違いとして統一して解釈できるようになったという経緯である。「電磁波は波長が違うと呼称が変化する」というのが答えのように思えるが、「波長が違うとなぜ呼称が変化するか」の答えにはならない。問いと答えがループしていて、根本的な答えには決してなっていない。
電波、赤外線、紫外線という言葉と概念は、電磁波という概念の前に存在していた。だから異なる呼称は歴史的な経緯ともいえるが、異なる呼称を使用するのが「当然」と考えられていた理由はそれらが別物と解釈されていたからだ。なぜ別物と考えられていたかと言えば、性質が違うからだ。呼称問題はこれで解決となるが、最後に「波長が変わると性質が変わるのはなぜか?」という問いが残る。この問いは少しの考察で到達できるとても根源的で哲学的な大問題なのだが、実際にはほとんど語られることはない。
科学とくに物理学ではなるべく少ない仮定で世界を解釈するというのが命題の一つである。可視光と電波の統合は大勝利である。しかし、当時の多くの学者は、とてもびっくりしたはずだ。まさか可視光と電波の実体が同じものとは思っていなかったに違いない。でなければ、可視光と電波を総称する固有の名前が存在したはずだ。電磁波という概念の大勝利に伴う万能感によって、些末な問題は吹き飛んでしまうものだ。
その些末の問題、可視光と電波を別物とみなしていた理由は簡単で、それらの性質が大きく異なるからだ。電波は電気回路から放射され、アンテナ(電線)で受け取ることができる。厳密には可視光でも似たような現象は生じるが、その現象は規模が小さいので、その存在を知っていないと調べようとも思わない。光は紙や木の板で遮ることができるが、電波はそれらを簡単に透過する。可視光と電波はなぜこんなにも性質が違うのだろうか?性質が違うから、可視光と電波は別物と考えられていて、それは異なる呼称を持つに至った理由として自然である。
可視光の周辺には赤外線と紫外線がある。いずれも目には見えない。なので、目には見えなくて可視光より波長が長いものを赤外線、短いものを紫外線と呼んでいる。光をプリズムで分光したとき、赤外線は赤い光の外側の場所に到達する目に見えない光として名付けられ、紫外線は紫の光の外側の目に見えない光として名付けられている。目に見えないという基準は実は物理学的にはあまり意味はない。多くの昆虫は紫外線を見ることができ、一部の蛇は赤外線を感知することができる。つまり、紫外線や赤外線が見えないというのは人間の生物としての能力に依存しており、別の生物では定義が変わってくる。つまり、生物種依存性であって、それは物理学が感知するような話ではない。
ちなみに、数学は「宇宙の法則が変化しても正しく」、物理学は「宇宙のどこでも正しく」、生物学は「地球上では正しく」、人文科学は「人間(文明・社会)に関しては正しい」ということで分類される。生物種に依存する議論は物理学の範疇にはないということである。
とは言うものの、赤外線は当たるとあったかくて、日焼けしない。逆に紫外線は火傷や日焼けをするけど、あったかくはない。そして可視光はあったかくもないし日焼けもしないが、目で見ることができる。明らかに性質が異なる。この性質の違いがあるからこそ、紫外線や赤外線の定義が生物種依存であるにもかかわらず、生物学以外の文脈でも受け入れられている。では、紫外線や赤外線の性質の違いは何に由来するのだろうか?電波との違いも同じように説明できるのではないか?もっと波長の短い領域、X線やガンマ線も同じように説明できるかもしれないと考えるのはやりすぎだろうか?
結論から言えば、電磁波は波長によって相互作用する相手が変化し、それゆえ性質が変化したように見え、それに応じて呼称が変化するということである。IRで用いられる赤外線は特に有機化合物中の分子内運動と相互作用する。赤外線にさらされた分子内運動は赤外線を吸収し、エネルギー保存則によって当該分子内運動が激しくなる。分子運動は熱であり温度であるので、赤外線を吸収することで有機化合物は温度が上昇する。その有機化合物が僕たちの体を構成するものであれば、僕たちはあったかいと感じる。
紫外線は波長にもよるが、二重結合と相互作用しやすいと考えるとよい。紫外線を吸収した二重結合はエネルギー準位が上がって、化学反応しやすい活性化状態に変化したり、結合が切れやすい反結合性軌道に変化したりする。これが僕たちの体で生じると制御されていない化学反応を生じ、体を傷つける。この現象は火傷と同じような症状を引き起こす。体にとっては害なので、体の防御反応として紫外線をシールドするための色素が形成される。これが日焼けである。紫外線で生じる反応は火傷と同じ症状なので、紫外線が当たると熱も感じることになる。しかし、これは生物的な反応なので、対象が生物でなければ熱を感じないし、その熱は化学反応の熱であって、物体を温めるようなものではない。ということで紫外線は暖房には使えない。
紫外線や赤外線が目に見えず、可視光だけが目に見える理由は、我々の視細胞の中にある色素の特性によるものである。人間の視細胞中の色素(オプシン)は3種類あり、それぞれ赤・緑・青の光に対するフィルターの役割がある。フィルターを通した光をレチナールという分子が受けると、色素中の特定の二重結合がシス・トランス転移を起こす。色素が構造転移すると視細胞が活性化し、脳に電気信号を送る。このメカニズムによって我々は視覚を得ている。赤外線や紫外線が見えないのは、レチナールの共役系がいい感じになっていて、可視光域(主に赤色)に対してシス・トランス転移する容認っているからである。おそらく、赤外線は量子力学的な理由で構造転移を起こさないし、紫外線はシス・トランス転移を引き起こすにはエネルギーが高すぎるのだと思われる。ちなみにオプシンはタンパク質であり、普通の人は赤青緑の3種類持っている。3種類あるから、光は「三原色」であり、色域チャートは三角おにぎりみたいな形をしている。
電波は金属などの中にある自由電子と相互作用する。金属中の電子は、複数の金属原子と共有されたエネルギー準位を持っていて、エネルギー準位間のギャップがとても小さい。ギャップが小さいので熱エネルギーのようなちょっとしたことがきっかけで金属原子の束縛を離れ、移動できるようになる。これが自由電子である。自由電子が熱的に励起されて移動することで、自由電子は熱のキャリアとして機能する。そのため金属の熱伝導率は高くなる。また、光が金属に当たるだけで大量の自由電子が発生する。これは金属光沢の起原となっている。白川英樹先生が実験失敗に思えた黒光りするポリアセチレンの小片を見て導電性を測定してみようと思い立ったのは、ポリアセチレンの小片に見られた金属光沢から自由電子の存在を見抜いたからである。自由電子は電気のキャリアなので、自由電子の存在は高い導電性を示唆するからである。
後述するが電波の持つエネルギーは実はとても小さい。とても小さいのでほとんどの物質と相互作用できない。唯一といってよいくらいの相互作用対象は金属中の自由電子である。なので、電波が金属に吸収されると金属中の自由電子を揺り動かし、電位を発生させる。こうして発生させた電位を検出することで、我々は電波を情報のやり取りに利用している。
まとめると、電磁波の名前が変化するのは、周波数によって相互作用する対象が変化するからだ、ということである。
相互作用の周波数選択性
電磁波の波長あるいは周波数が違うと生じる「現象」が違うようだとわかる。「現象」と波長あるいは周波数の関係は「個別案件」なのかそれとも法則性があるのだろうか?当然、法則性があったら良いな、と思うわけである。
公園の遊具の定番であるブランコで遊んだことのない人は皆無だろう。小さい子供は体重移動をうまく行えないので、別の人に背中を押してもらってブランコで遊ぶことになる。背中を押してもらうとブランコの振幅が増加する。ブランコにおいて振幅が増加するとは、ブランコの振動に関する運動エネルギーが増加したとみなすことができる。増加した運動エネルギーの源は当然背中を押す行為である。つまり、ブランコの背中を押すという行為は、背中を押す人からブランコに乗っている人へのエネルギー移動であると解釈できる。これをもっと物理学の言葉を使って表すなら、背中を押す人とブランコが相互作用した結果、エネルギーが移動した、となる。
ブランコの背中を押す際に大事なのは、ブランコの振動に合わせてタイミングよく背中を押すということである。エネルギーの受け手であるブランコの振動数と、エネルギーの源である背中を押す行為の振動数が一致するときに、エネルギーの移動効率が最大になることは自明に見える。このような現象は物理学では共鳴と呼ばれている。
このブランコの例に似たような現象はSPring-8などの放射光における電子線の加速に利用されているRF加速器の原理にもみられる。RF加速器では高速で移動する電子に周期的な電場の振動を加えると、タイミングが合っていれば電子が加速される。電場の波に対して電子がサーフィンする感じで、電子は加速される。SPring-8の普及棟という一般向け啓蒙施設に模型があって、RF加速器の原理を体験できるので、ぜひ体験してほしい。電場の波のタイミングが合わないと電子は加速しない。これはブランコで背中を押すのと似ている。
赤外線は電磁波であり、電場の振動である。原子や電子は電荷をもっているので、赤外線の電場の振動のタイミングが合えば、RF加速器と同じような原理で原子や電子は加速される。物質、特に有機分子中では、原子は伸縮とか変角とかいった特定の分子内運動をしている。その運動と電場の振動のタイミングが合うと分子運動が加速される。分子運動が加速されるということは、その分子運動のエネルギーが増加するということ。つまり、電場(赤外線)から物質にエネルギーが移動した=赤外線が物質に吸収された、となる。IRはこうしたプロセスによる赤外線の吸収を観測している。赤外線の電場の振動数$\nu$は、$\lambda\nu=c$であるので、波数は$\lambda^{-1}=\nu/c$である。分子運動の振動数が一致するときにエネルギーの移動確率が最大になる。
光は量子化されており、エネルギーは光子エネルギーの単位でやり取りされるというのが原則だ。なので、赤外線の吸収においても、1回の相互作用において、赤外線の光子エネルギー$h\nu$の単位で分子運動にエネルギーが移動する。この現象は、分子運動には固有の振動エネルギー$h\nu$を単位として相互作用する、というように見ることもできる。振動数の一致で説明するか、エネルギーの一致で説明するかの2択ではなく、(特に赤外線の領域では)どちらの解釈でも本質は変わらない。振動数が一致するときに$h\nu$を単位としてエネルギー交換するのだから。
かくして、ブランコの例にあるように振動数の一致による相互作用確率の最大化という現象は、エネルギーの一致による相互作用の最大化と解釈できるということになる。これはあたかも量子力学において、エネルギー準位による相互作用の選択と同じようだ。量子力学ではエネルギーを与える側が受け取る側よりエネルギーが小さいと相互作用が全く起こらないという非対称なルールが追加されるという点が異なるが、本質はほとんど変わらない。振動数の一致による相互作用は、厳密には「共鳴」と呼ばれることが多い。
相互作用の確率は「振動数が一致」=「エネルギーが一致」=「波長が一致」するときに最大になるというが極めて一般的なルールであることがわかる。なので、電磁波の呼称に波長依存性があるのは、この相互作用確率に応じて相互作用に関係する事象の選択が生じていることが根本的な理由と言える。
赤外線領域に関する相互作用は、分子内振動のもとになっている原子間の結合力と結合している原子の重さによって決まる固有振動の振動数が、ちょうど赤外線の振動数に近いため、赤外線は分子運動によって吸収される。紫外線領域では二重結合あるいは共役系が持つエネルギー準位がちょうど紫外線の光子エネルギーに一致するので、これらの化学結合が紫外線をよく吸収し、エネルギー準位が上がる。このプロセスは量子力学に従うので、光子エネルギーが低い赤外線では相互作用が起こらない。逆に、紫外線の光子エネルギーは赤外線と相互作用する分子運動とはエネルギーが大きく異なるので、相互作用確率が著しく低い。そのため、紫外線では物体を温める効果は期待できない。
X線くらい波長が短い=エネルギーが高いと、原子の周囲に強く束縛されている電子と相互作用できるようになる。もっとエネルギーが高いガンマ線は原子核と相互作用し、核化学的な反応を引き起こす。これはちょっとした核反応であり、化学的な方法では制御できないため、とても厄介である。
金属結晶では複数の金属原子が波動関数を共有し、エネルギー準位が細かく分割される。そのため、Highest Occupied Molecular Orbital(HOMO)とLowest Unoccupied Molecular Orbital(LUMO)のエネルギー差がとても小さくなる。本来はHOMOでじっとしているはずの電子は、ちょっとしたことでLUMOに上がってしまい、金属原子の束縛を離れて移動できるようになる。これが自由電子である。HOMOからLUMOのエネルギー差はとても小さいのでいろんな理由で電子が移動することになる。電波の波長はとても長く、時には数百メートルにもなる。振動数は小さく、エネルギーも小さい。エネルギーの小さな電波はこれまで議論してきた理由によって相互作用できる相手が多くない。そんな電波でも自由電子は相互作用できる。というか自由電子のエネルギー準位はちょうど電波くらいなのだ。電波は金属中の自由電子を移動させる。電子の移動は電位を生じ、その電位を計測することで僕たちは電波を検出できる。電波を受信するアンテナが金属なのはこうした理由による。
まとめると、相互作用とはエネルギーの移動現象であり、エネルギーの移動の確率は周波数∝エネルギー∝波数∝波長の逆数、に強い依存性がある、ということである。
異なる分光法が同じ情報を与える
X線の吸収分光の一つにX線吸収微細構造(X-ray Absorption Fine Structure, XAFS)がある。XAFSのデータは測定範囲等も含めて電子線損失分光法(Electron Energy Loss Spectroscopy, EELS)と等価であることが知られている。XAFSはX線を用いた透過吸収スペクトルである。IRのX線バージョンと考えてよい。物質内にX線の光子エネルギーと同じエネルギー準位が存在すれば、強い吸収が生じる。物質内のエネルギー準位はX線領域では、物質を構成している元素を強く反映している。さらにXAFSでは元素同士の結合に寄与するような最外殻電子のエネルギー準位の情報も得ることができ、測定対象の様々な情報が得られる。
一方、EELSは加速された電子(電子線)が物質と相互作用して、電子線の持つエネルギーの一部が物質に吸収される。その結果、電子線は物質に吸収された分だけエネルギーを失ってしまう。この失ったエネルギーをスペクトルとして表したものがEELSである。EELSは現象がやや複雑であるが、物質との相互作用は量子化されており、EELSは物質内のエネルギー準位を表すことになる。EELSで利用している現象は非弾性散乱の一種であり、この話を語りだすととても長くなるので、ここでは割愛する。
片やX線、片や電子線。片や単純吸収分光、片や非弾性散乱と、かなり違っているにもかかわらず、両者の測定データは詳細は異なるものの、等価である。特にX線領域での分光法ではこのような等価性が多く知られている。X線を入射して蛍光X線を観測する蛍光X線分光法、電子線を入射して蛍光X線を観測するエネルギー分散型X線分光装置(Energy Dispersive X-ray Spectroscopy, EDX、SEMのオプション検出器としてよく知られている)、X線を入射して飛び出てくる電子線を観測するX線電子分光法(X-ray Photoelectron Spectroscopy, XPS)、電子線を入射して飛び出てくる電子を観測するオージェ電子分光法(Auger electron spectroscopy, AES)。これらの測定データはほとんど同じような情報を与える。電子線を入射する場合、あるいは電子を観測する場合は概ね試料の表層の情報となるが、X線を入射してX線を観測する場合は、比較的試料内部の情報が得られる傾向がある。電子線は細く絞ることができるので、電子線を入射する場合には測定に空間分解能を期待できる。言い換えると、顕微鏡法と組み合わせることができる、ということになる。そうしたこまごました違いがあるものの、測定対象の構成元素に関する情報が得られるという点でこれらの方法は同じだし、横軸にエネルギーの単位である$eV$(あるいは$KeV$)を採用するという共通点がある。なぜこのような共通点を持つのだろうか?それは偶然か、必然か?
結論は簡単で、X線や電子線に関わらず相互作用の対象が同じだから、である。同じ相互作用の有無を見ていながら、結果が違う方が大問題である。ただ、一つ問題になるのは、エネルギーの源が電磁波や電子と全く異なる、ということである。
透過型電子顕微鏡は電子線の持つ物質波を光の代わりに用いて作られた顕微鏡である。光速に運動する電子は物質波を纏うようになるというのが高校物理での説明だ。この物質波を通して電子は光と同じように物質と相互作用できるというのが量子力学の考え方である。なので、相互作用する際のエネルギーの源は電子であっても光であっても構わない。もっと言えば、中性子などであっても構わない。もちろん、相互作用する確率の比例係数はちょっと違ってくるが、エネルギーの選択性は変わらない。深く考えてゆくと物質波とは何か?という問題にぶち当たるが、物質波の本質についての議論も長くなるので、ほかに譲る。
相互作用する際の原理のようなものが多少違っても相互作用する相手が同じならば同じ情報が得られる、という事例は普通の光の領域においても知られている。IRとラマン分光法で等価な情報が得られる有名だ。IRでは赤外線の吸収、ラマン分光法では可視光の非弾性散乱を測定している。どちらも光を用いた分光法であるが、波長が大きく異なる。また、ラマン分光法が用いる非弾性散乱という現象は原理がとても分かりにくい。
非弾性散乱は入射光が物質と相互作用して波長が少し長くなった光を散乱波として再放出する現象である。波長が少し長くなるとか、散乱派として再放出するという性質は蛍光ととても似ている。非弾性散乱が蛍光と異なるのは、入射光の波長選択性がほとんどないことである。ラマン分光法では試料に入射する光の波長は基本的に何でもよい。通常の実験条件であれば可視光域であればだいたい大丈夫で、試料の特性に応じて入射光の波長を調整することすらある。
光が物質と相互作用する通常のケースは、例えばIRのように、入射光の振動数と物質内の何らかの振動の振動数が一致する場合である。一致する場合に相互作用確率が最大になる。入射光の振動数が物質内の振動数より小さい場合には、その相互作用メカニズムが量子力学的であれば、相互作用確率が0になる。物質内の振動数の方が小さい場合には、入射光の振動数と物質内の振動数の差に概ね反比例するような確率で相互作用する。その相互作用では入射光から物質内の振動にエネルギーが移動する。相互作用する際のエネルギーの単位は当然物質内の振動のエネルギー準位であるので、入射光は物質内の振動のエネルギー準位(典型的には)1個分のエネルギーを失うことになる。光は量子化されているので、エネルギーを失うということは、光子で考えると振動数が低下する=波長が長くなることになる。この低確率で生じる振動数が不一致な相互作用を測定するのがラマン分光法である。相互作用に関与する物質内の振動がちょうどIRで観測されるような振動であるので、ラマン分光法のデータはIRのデータと互換性がある。
まとめると、分光法では相互作用する対象が同じであれば、測定方法が違っていても同じ情報が得られる、というのが割と一般的な法則である、ということだ。
「分光法」の再定義
これまでの議論から、分光法では(主に)光と物質内の振動要素との相互作用を、振動数・波数・波長・光子エネルギーなどを掃引して調査する、と総括することができる。しかも、振動数、波数、波長はすべて(光子)エネルギーに読み替えることができることから、分光法では相互作用に伴うエネルギーのやり取りの確率を測定しているのだと理解できる。逆に言えば、分光法とは相互作用の周波数(エネルギー)依存性を明らかにすることであると再定義できるだろう。
レオロジー測定では光は一切関与しないし、得られるのは粘弾性スペクトルであり、横軸は(角)周波数ではあるが縦軸は複素数である。まだ分光法とは隔たりがある。レオロジーの粘弾性スペクトルは、別名を緩和スペクトルと言う。緩和スペクトルという名称は粘弾性スペクトルを含むいくつかの測定において共通する名称である。
「緩和」という言葉には、何かが時間をかけて「減衰」する、というイメージがある。典型的な粘弾性スペクトル測定では、弾性率や応力の「減衰」を直接観測するわけではない(そのような実験方法も存在する)ので、緩和スペクトルと言う語は適切でない気もする。この議論を進めるには「緩和」という言葉を物理学の概念で再定義する必要がある。
「減衰」という言葉で思い浮かぶ現象の一つに、摩擦によって運動が停止する、という物理の大学入試でよく出てくる現象がある。物体が直線運動するときに摩擦が働くと速度が減衰し、運動が停止する。このとき、物体の運動エネルギーは摩擦を通じて失われ、基本的には熱として散逸する。
他の「減衰」の事例として、単振動しているバネ・おもり系が、空気抵抗やバネ内部の原子間の「摩擦」によって、振幅が小さくなる現象が思い当たる。空気抵抗も「摩擦」の一種なので、主に「摩擦」によってバネ・おもりの単振動が「減衰」すると言える。バネ・おもりの単振動では、バネの伸びによって生じる位置エネルギーとおもりの運動エネルギーが相互に変換され続けるが、減衰しない場合のトータルのエネルギーは一定である。トータルのエネルギーは概ね振幅の2乗に比例する。「摩擦」によって単振動が「減衰」する場合、振幅が徐々に小さくなるので、トータルのエネルギーは減少することになる。つまり、「減衰」では、摩擦を通じてエネルギーが失われるということである。
これらの事例を通じて、緩和≒減衰≒エネルギーが失われること、というイメージが湧いてくる。我々が日常的に観測している世界ではエネルギーは保存するので、エネルギーが世界から無くなることはなくて、「失われたエネルギー」は別の形態のエネルギーに変化しただけである。ここから、緩和≒エネルギーが移動すること、と大雑把に短絡することができるだろう。
レオロジー測定で得られる複素弾性率の虚数成分は、入力された弾性エネルギーの吸収を表すことが簡単な計算によって示されている。詳細は長くなるのでここでは割愛するが、複素弾性率の虚数成分を実数成分で除した値を$\tan \delta$と呼び、ちょうどこれは「入力された弾性エネルギーの何割を材料が吸収するか」という指標になる。つまり、レオロジー測定で$\tan \delta$を計測し、入力弾性波の周波数でプロットすれば、IRと同じように吸収スペクトルになっているということである。
レオロジーの分野では詳しく説明されることはないが、粘弾性スペクトルで観測されるエネルギー吸収のメカニズムは基本的に何でも良い、というのが研究者たちの共通認識になっている。エネルギー吸収のメカニズムに応じて特定の周波数での吸収が観測される。これはあたかも、通常の分光法における特徴と同じである。すなわち、「分光法では相互作用する対象が同じであれば、測定方法が違っていても同じ情報が得られる」「エネルギーの移動の確率は周波数∝エネルギー∝波数∝波長の逆数、に強い依存性がある」という特徴と完全に一致している。
さらに、レオロジー測定で得られる粘弾性スペクトルと同じ情報が、誘電緩和測定によって得られることが良く知られている。なぜそのような関係があるのかについてレオロジーの分野では詳しく説明されることはないが、レオロジー測定や誘電緩和測定が分光法と同じ特徴があると考えれば、すんなり腑に落ちる。誘電緩和測定で得られるデータは誘電緩和スペクトルと呼ばれ、粘弾性スペクトルと同様に実部と虚部のある複素誘電率のグラフになる。誘電緩和は試料の両側に電極を取り付け、片側にサイン波の電圧をかけ、反対側の電極の電圧を計測する。計測される電圧は入力のサイン波と比べて、振幅や位相が異なる。これを解析して複素数の誘電率を決定する。入力波の周波数を変えて測定を繰り返すスペクトルを得る。これはレオロジー測定とほとんど同じフォーマット持つことがわかるだろう。
高周波領域の誘電緩和測定では、「電波」を利用して測定が行われる。マイクロストリップラインという計測方法では、試料の片側に線状の電極を取り付けて(精度を求めて蒸着することが多い)、その線に周期的に変化する電流を流す。ビオサバールの法則に従い、電流は周囲に周期的に変化する電磁場(電波)を作り出す。その電場と試料(表面)が相互作用することで、電流に影響が生じる。その影響を配線の電位として計測する。解析することで、GHz領域の誘電緩和スペクトルが得られる。
マイクロストリップラインを用いた誘電緩和測定は電波領域の電磁波を利用した測定となっており、電波による分光法の一形態とみなせるかもしれない。だから、誘電緩和測定を分光法の文脈で解釈することができないとつじつまが合わないことになる。周波数が異なるだけで同じ情報が得られるのだから、通常周波数帯の誘電緩和測定やそれと等価な情報が得られるレオロジー測定も分光法の文脈で理解できるはずだ。
繰り返しになるが、「分光法とは相互作用の周波数(エネルギー)依存性を明らかにすることである」とするなら、IR、NMR、XAFS、EELS、レオロジー測定、誘電緩和測定などこのエッセイで登場した測定法がすべて分光法に分類できることになる。だから、レオロジー測定は分光法か?に対する答えはYESとなる。
ヒッグス粒子の探索
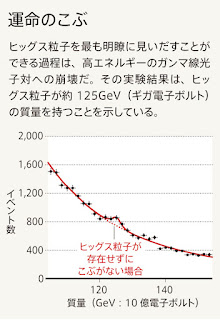
話は少し変わるが、分光法に対するこうした理解が助けになる事例を紹介しよう。スイスのCERNにある大型ハドロン衝突器(Large Hadron Collider, LHC)で行われたヒッグス粒子の探索はほぼ成功し、 Peter Higgs先生らがノーベル賞を受賞した。その際、粒子をぶつけてヒッグス粒子を探すという考え方に違和感を持たなかったろうか?ヒッグス粒子は存在が不確定でその性質もよくわかっていない。なのに粒子を勢いよくぶつけたら、その存在を確認できるなんて、とても乱暴な話だ。そんな乱暴でふわっとした話にもかかわらず、ものすごいお金が投入されることになった。成功確率はどのくらいだったのだろう?それに、何かを見つけたとして、どうしてそれがヒッグス粒子に関わるものだと断言できるのだろう?
ヒッグス粒子の証拠として発表されたのが上の図である。125GeVあたりにこぶがあって、これがヒッグス粒子のエネルギーの予測範囲になることから、このこぶがヒッグス粒子の存在を示すとされた。縦軸はイベントとなっており、一瞬何かの粒子ができてすぐに崩壊したときの崩壊のエネルギーを横軸にとっている。要は、粒子衝突して、ピカッと光るんだけど、そのピカッとした光のエネルギーが横軸である。素粒子物理学は物理学の超天才たちが鎬を削る選ばれた人々だけの世界なんで、このグラフがヒッグス粒子の存在を示していると言われても因果関係はさっぱり理解できなくても別に何とも思わないかもしれない。とっても難しい理論が背景にあって、一般人には決して理解できないんだろうな、とか思ってしまう。
いろんな解説記事はネット上に存在するけど、ヒッグス粒子を確認したことの意義とかそういうのはいっぱい出てくるけど、このグラフが何を意味しているのかはちゃんと説明がない。そもそも、何を測定しているのかすらわからない。このグラフは素粒子が崩壊する現象をカウントし、崩壊時に発生するエネルギーを調べる実験の結果である。素粒子はとても寿命が短いので、何かの原因で素粒子ができてもすぐに崩壊して光(多くはガンマ線)になってしまう。だから崩壊するのは自然なことで、検出はそれを利用している。素粒子の崩壊以外でも光は出てくるのだが、素粒子が持っているスピンなどの保存量が崩壊前後で保存されなければならないという条件から、多くの素粒子は2つの光子を互いに反対の方向に同時に生成(光子対)する。この現象は陽電子放出断層像(Positron Emission Tomography, PET)などでも用いられており、割と普通の現象である。なので、素粒子崩壊によって生じた光かどうかは、反対側にも同時に光が観測されたかどうかを確認すればよい。崩壊のもとになった素粒子のエネルギーは対になった光子の合計である。上の図のキャプションにも「光子対」の言葉を確認できる。ということで、上の図はどういうエネルギーの素粒子が崩壊したか、その数はどうか、というグラフということである。
素粒子が崩壊するためには素粒子が存在しないといけない。ほとんどの素粒子はとても寿命が短いので、通常は何かがきっかけで生成されなければならない。素粒子が生成されたきっかけははっきりしていて、LHCが起こした粒子衝突である。
LHCによる粒子衝突であるが、ヒッグス粒子は直接関係しない。衝突に関与するのは加速された粒子(原子)と衝突された粒子(原子)だから、それらが素材となっている。普通に考えると素材からヒッグス粒子が生成されたと思うところだが、実はそうではない。ぶっちゃけると素材となった粒子は基本的にヒッグス粒子とは無関係だ。重要なのは衝突で生まれるエネルギーだ。実はヒッグス粒子は真空であっても空間内にひっそりと詰まっているらしい(僕はこの説明がエーテル宇宙論的なんで好みではない)。だから、何もない空間であってもエネルギーがあったら真空からポコンとヒッグス粒子が飛び出してくるそうだ。これはあたかも、金属表面に光を当てると光電効果によって電子が飛び出す現象にそっくりだ。XPSはこの原理を使った測定で、金属などの束縛エネルギーがわかる。LHCの粒子衝突では飛び出した素粒子のエネルギーを観測することになる。LHCは真空にエネルギーを衝突させて、真空がエネルギーを吸収して素粒子を飛び出させるという現象を使って、ヒッグス粒子を見つけたということだ。これはまさに分光法である。試料は真空で、入力は粒子衝突のエネルギーという突拍子もないものではある。
分光法だと理解すれば、話は簡単で受け入れやすい。素粒子生成の細かなメカニズムを考える必要はないし、入力も何らかのエネルギーであれば何でも良い。量子力学が支配する領域の現象なので、入力は光かエネルギーかの2択になる。あまりに高エネルギーの光は作ることが難しいので、LHCレベルであれば、入力はエネルギー1択になる。エネルギーの生成法も特に制限がないので、人類が用意できる最高レベルのエネルギーとして粒子加速器2つを使った正面衝突ということになったのだろう。LHCの前には粒子に陽電子を衝突させていたはずだ。陽電子は軽いので、ハドロン(要は、プロトン)を使うことにしたという割と安直な考えのようだ。素粒子物理学の最先端の話で門外漢には全く理解できない話だと思っていたが、分光法だと気づけば案外わかる話のようだ。
波及効果に関するコメント
粘弾性スペクトルや誘電緩和スペクトルと同じように周波数依存性を持つ複素数の測定値と言えば、インピーダンスがある。もちろん、インピーダンス測定も一種の「分光法」ということになる。これらすべては条件を満たせば線形応答理論に従うという共通点を持っている。
線形応答理論は、入力と出力を持つ独立した系(システム)すべてに適用できる極めて広い概念である。線形応答理論が適用対象となる条件は、①入力がなければ出力もない。②入力と出力に比例関係がある。③システムは入力以外の影響を受けない。の3つである。①の条件は、ある種の因果律で、これに従わない出力はノイズである。②の条件は入力が十分小さければ必ず成立する。これはあらゆる関数がマクローリン展開できるという数学的事実と対応している。③はシステムが独立であるということを言い換えたに過ぎないが、物理的には入力と出力とシステム(内部)の間でエネルギー保存が常に成り立つという条件を課すことになる。まとめると、線形応答理論は、数学と因果律とエネルギー保存に基づいており、僕たちがこうした事柄に異を唱えない限り受け入れなければならない法則と考えてよい。
線形応答理論の帰結として、システムを表す物理量(係数)は必ず複素数になり、周波数依存性を持つ。だから、粘弾性・誘電率・インピーダンスはいずれも複素数であり、スペクトルになる。周波数依存性を持つので(入力・システム間の)相互作用に周波数依存性が現れる。
IRに代表されるような「吸収」現象も本当のところは複素数であり周波数を依存性をもつと考えるべきだろう。IRの吸収も、粘弾性スペクトルにおける$\tan \delta$のようなもので、そのもととなる複素数の物理量が存在するはずだ。ま、実際のところ、誘電緩和測定をIR領域の周波数で行うことができれば、IRと誘電緩和測定はおそらく完全に一致する。
IR領域で本来存在するはずの複素数量を測定するには、波の解析をして位相のシフトを観測しないといけない。IR領域では波を直接測定できないし、位相は試料のちょっとした凹凸で大きく変化してしまう(干渉計を使えば位相を求められるはずだが、IR領域で機能する干渉計を組み立てて調整するのはなかなか大変だと思われる)。だから、IR領域では材料に由来する位相の変化を測定することは難しい。逆に、粘弾性・誘電率・インピーダンスは波の直接測定が可能なので、複素数量の決定が可能であるだけだと解釈できる。
数学は受け入れないと始まらない。因果律を否定したら科学全体が立脚している客観性が崩壊する。エネルギー保存を否定したらほとんどの物理が意味をなさなくなる。数学・因果律・エネルギー保存から、分光法が立脚する基本原理が導かれるのであるから、分光法の概念は物理に根深く埋め込まれているということになる。
ということでこのエッセイが広げる風呂敷はとても大きい。大きすぎるので僕という非才がちゃんとした論文で議論するには重すぎる。なのでエッセイという形でご容赦いただきたい。